-
The figure below represents part of a tape pulled through a ticker-timer by a trolley moving down an inclined plane. If the frequency of the...
(Solved)
The figure below represents part of a tape pulled through a ticker-timer by a trolley moving down an inclined plane. If the frequency of the ticker-timer is 50Hz, calculate the acceleration of the trolley.

Date posted:
April 23, 2019
.
Answers (1)
-
A paper tape was attached to a moving trolley and allowed to run through a ticker-timer. The figure below shows a section of the tape.
(Solved)
A paper tape was attached to a moving trolley and allowed to run through a ticker-timer. The figure below shows a section of the tape.

If the frequency of the ticker-timer is 20Hz, determine:
a) The velocity between AB and CD.
b) The acceleration of the trolley.
Date posted:
April 23, 2019
.
Answers (1)
-
A machine with a velocity ratio of 30 moves a load of 300N when an effort of 200N is applied. Calculate the efficiency of the...
(Solved)
A machine with a velocity ratio of 30 moves a load of 300N when an effort of 200N is applied. Calculate the efficiency of the machine.
Date posted:
April 22, 2019
.
Answers (1)
-
Explain why a man using a parachute falls through air slowly while a stone falls through air very fast
(Solved)
Explain why a man using a parachute falls through air slowly while a stone falls through air very fast.
Date posted:
April 22, 2019
.
Answers (1)
-
A man makes a deeper marks while walking on a soft ground in a high heeled shoes than in a flat shoes. Explain
(Solved)
A man makes a deeper marks while walking on a soft ground in a high heeled shoes than in a flat shoes. Explain
Date posted:
April 22, 2019
.
Answers (1)
-
Explain how temperature affects Brownian motion
(Solved)
Explain how temperature affects Brownian motion.
Date posted:
April 18, 2019
.
Answers (1)
-
Discuss the Maintenance of the Accumulators
(Solved)
Discuss the Maintenance of the Accumulators
Date posted:
April 15, 2019
.
Answers (1)
-
Define Electromotive Force (E.m.f) and Potential Difference
(Solved)
Define Electromotive Force (E.m.f) and Potential Difference
Date posted:
April 15, 2019
.
Answers (1)
-
Explain the applications of Thermal Radiation
(Solved)
Explain the applications of Thermal Radiation
Date posted:
April 15, 2019
.
Answers (1)
-
Explain the mode of Operation of the Six’s Thermometer
(Solved)
Explain the mode of Operation of the Six’s Thermometer
Date posted:
April 15, 2019
.
Answers (1)
-
Give the comparison between Mercury and Alcohol as Thermometric Liquids
(Solved)
Give the comparison between Mercury and Alcohol as Thermometric Liquids
Date posted:
April 15, 2019
.
Answers (1)
-
The height, h of a water manometer is 20 cm when used to measure pressure of a gas.
(Solved)
The height, h of a water manometer is 20 cm when used to measure pressure of a gas.
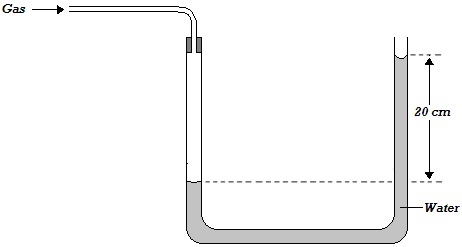
a) Determine the pressure due to gas, If atmospheric pressure is 103000N/m2.
b) What would be the height if the liquid used is glycerin of density 1.26g/cm3
Date posted:
April 15, 2019
.
Answers (1)
-
A sphere of diameter 6.0 mm is molded into a uniform wire of diameter 0.2mm. Calculate the length of the wire.
(Solved)
A sphere of diameter 6.0 mm is molded into a uniform wire of diameter 0.2mm. Calculate the length of the wire.
Date posted:
April 15, 2019
.
Answers (1)
-
An object whose area of contact with the floor is 5m2 exerts a pressure of 900 pascal
(Solved)
An object whose area of contact with the floor is 5m2 exerts a pressure of 900 pascal. Calculate its mass
Date posted:
April 15, 2019
.
Answers (1)
-
A mixture consists of 40cm3 of water and 60cm3 of liquid X. If the densities of water and liquid X are 1.0g/cm3 and 0.8g/cm3 respectively,...
(Solved)
A mixture consists of 40cm3 of water and 60cm3 of liquid X. If the densities of water and liquid X are 1.0g/cm3 and 0.8g/cm3 respectively, calculate the density of the mixture.
Date posted:
April 15, 2019
.
Answers (1)
-
The mass of a density bottle is 20.0g when empty, 70.0g when full of water and 55.0g when full of a second liquid x. Calculate...
(Solved)
The mass of a density bottle is 20.0g when empty, 70.0g when full of water and 55.0g when full of a second liquid x. Calculate the density of the liquid (take density of water to be 1g/cm3)
Date posted:
April 15, 2019
.
Answers (1)
-
A wooden block of mass 200g is 4.0 cm wide 3.0 cm thick and 6.0 cm long. Calculate the density of the wooden block in...
(Solved)
A wooden block of mass 200g is 4.0 cm wide 3.0 cm thick and 6.0 cm long. Calculate the density of the wooden block in kg/m3
Date posted:
April 15, 2019
.
Answers (1)
-
What are the advantages of Electrical Balance (Top Pan Balance) Over the Beam Balance (Mechanical Type)?
(Solved)
What are the advantages of Electrical Balance (Top Pan Balance) Over the Beam Balance (Mechanical Type)?
Date posted:
April 15, 2019
.
Answers (1)
-
State the conditions under which displacement method works
(Solved)
State the conditions under which displacement method works
Date posted:
April 15, 2019
.
Answers (1)
-
Find the volume of a sphere whose radius is 3.0cm
(Solved)
Find the volume of a sphere whose radius is 3.0cm
Date posted:
April 15, 2019
.
Answers (1)