-
On the grid provided, draw the square whose vertices are A(6, -2), B(7, -2), C(7, -1) and D(6, -1).
(Solved)
On the grid provided, draw the square whose vertices are A(6, -2), B(7, -2), C(7, -1) and D(6, -1).
On the same grid, draw:
(i) A’B’C’D’ the image of ABCD, under an enlargement scale factor 3 centre (9, -4)
(ii) A"B”C”D” the image of A’B’C’D’ under a reflection in the line x = 0
(iii) A”’B’”C’”D’” the image of A”B”C”D” under a rotation of +90° about (0,0).
Date posted:
November 8, 2019
.
Answers (1)
-
A line L1 passes through the points (-2, 3) and (-1, 6) and is perpendicular to L2 at (-1, 6).
(Solved)
A line L1 passes through the points (-2, 3) and (-1, 6) and is perpendicular to L2 at (-1, 6).
a) Find the equation of L1.
b) Find the equation of L2 in the form ax + by - c = 0 where a, b and c are constants.
c) Given that another line L3 is parallel to L1 and passes through point (1,2) , find the x and y intercepts of L3 .
d) Find the point of intersection of L2 and L3.
Date posted:
November 8, 2019
.
Answers (1)
-
The diagram represents a solid frustum with base radius 21cm and top radius 14cm. The frustum is
22.5cm high and is made of a metal whose...
(Solved)
The diagram represents a solid frustum with base radius 21cm and top radius 14cm. The frustum is
22.5cm high and is made of a metal whose density is 3 𝑔⁄𝑐𝑚3. (Take 𝜋 = 22/7)
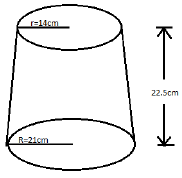
a) Calculate
(i) The volume of the metal in the frustum.
(ii) The mass of the frustum in kg.
b) The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost.
Calculate to 2 decimal places the length of each side of the cube.
Date posted:
November 8, 2019
.
Answers (1)
-
A number m is such that if its reciprocal is added to three times itself the result is 4. Form an equation in m and...
(Solved)
A number m is such that if its reciprocal is added to three times itself the result is 4. Form an equation in m and solve it.
Date posted:
November 8, 2019
.
Answers (1)
-
Find the area of the shaded region in the figure below given that AD = 15 cm, BE = 3 cm, AB = 3 cm,
???????...
(Solved)
Find the area of the shaded region in the figure below given that AD = 15 cm, BE = 3 cm, AB = 3 cm,
∠𝐷𝐴𝐵 = ∠𝐸𝐵𝐶 = 90°.
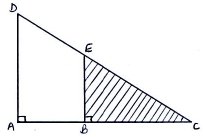
Date posted:
November 8, 2019
.
Answers (1)
-
A man sets off by bus on a journey of 130 km. after the bus has traveled 119 km at an average speed of 42...
(Solved)
A man sets off by bus on a journey of 130 km. after the bus has traveled 119 km at an average speed of 42 𝑘𝑚/ℎ𝑟, it breaks down and he is immediately given a lift by a passing cyclist who takes him to his destination at average speed of 66 km/h.
Calculate;
a) The time taken for the whole journey.
b) His average speed for the whole journey.
Date posted:
November 8, 2019
.
Answers (1)
-
(a) Using a ruler and a compass only, construct triangle ABC in which BC = 8 cm,
angle ABC = 30° and angle ACB = 45°...
(Solved)
(a) Using a ruler and a compass only, construct triangle ABC in which BC = 8 cm,
angle ABC = 30° and angle ACB = 45° .
(b) At A drop a perpendicular to meet BC at D and measure AD.
Date posted:
November 8, 2019
.
Answers (1)
-
The distance from A to B is d km and that from B to C is x km. if a bus maintains an average speed...
(Solved)
The distance from A to B is d km and that from B to C is x km. if a bus maintains an average speed of 50 km/h between A and B and 60 km/h between B and C, it takes 3 hours to travel from A to C. If it maintains 60 km/h between A and B and 50 km/h between B and C, the journey takes 8 minutes less.
What is the distance from A to C via B?
Date posted:
November 8, 2019
.
Answers (1)
-
A cylindrical tank of diameter 1.4 m and height 1.2 m is two – thirds full of water. The tank if filled using a cylindrical...
(Solved)
A cylindrical tank of diameter 1.4 m and height 1.2 m is two – thirds full of water. The tank if filled using a cylindrical bucket of diameter 35 cm and diameter 20 cm. Find the number of buckets required to fill the tank.
Date posted:
November 8, 2019
.
Answers (1)
-
Solve for x in the equation 125-x × 52(x-2) = 25(x+2)
(Solved)
Solve for x in the equation 125-x × 52(x-2) = 25(x+2)
Date posted:
November 8, 2019
.
Answers (1)
-
a) The first term of a geometric progression is 36. The sum of the first three terms is 27.
Calculate the common ratio and the value...
(Solved)
a) The first term of a geometric progression is 36. The sum of the first three terms is 27.
Calculate the common ratio and the value of the second term.
b) The first term of an AP is 2. The first term of a geometric sequence is also 2 and its common ratio
equals the common difference of the arithmetic sequence. The square of the fifth term of arithmetic
sequence exceeds the third term of the geometric sequence by 2. Find the common difference and the
sum of the first 50 terms of AP.
Date posted:
November 8, 2019
.
Answers (1)
-
Two towns on latitude 30oS are 3000km apart. Find the longitude different of the two towns
(Solved)
(a) Two towns on latitude 30oS are 3000km apart. Find the longitude different of the two towns
(Take 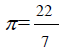 and the radius of the earth to be 6370km)
and the radius of the earth to be 6370km)
(b) The positions of airport P and Q are (60oN,45oN) and Q(60oN,KoE). It takes a plane 5 hrs to travel due east from P to Q at an average speed of 600 knots
(i) Calculate the value of K
(ii) The local time at P is 10.45am, what is the local time at Q when the plane reaches where?
(c) Calculate the shortest distance between (30oS,36oE) and (30oS,144oW) in nautical miles
Date posted:
November 8, 2019
.
Answers (1)
-
The cash price of a camera is Sh.42,200. Joseph bought the camera on hire purchase (H.P) term by paying a deposit of Sh.7,200 and cleared...
(Solved)
The cash price of a camera is Sh.42,200. Joseph bought the camera on hire purchase (H.P) term by paying a deposit of Sh.7,200 and cleared the balance in 24 equal monthly installments each of Sh.2,250
(a) Find the amount of interest paid under hire purchase plan
(b) Ken took a loan from a financial institution and bought the camera with cash. He repaid the loan in two years at 18% interest compound semi-annualy. Find the total interest paid by Ken
(c) The cash price is taken as the value of the Camera. If the camera depreciated at a rate of 15% in the first year after buying and at P% p.a for rest of the time, calculate the value of p if the value of the camera after 5 years was Sh.23,534
Date posted:
November 8, 2019
.
Answers (1)
-
(a) A sequence is formed by adding corresponding terms of an A.P and a G.P. The first, second and third terms of the sequence formed...
(Solved)
(a) A sequence is formed by adding corresponding terms of an A.P and a G.P. The first, second and third terms of the sequence formed after adding the first three terms of the sequences are 14,34 and 78 respectively. Given that the first term of the A.P is a and the first term of the G.P is b, and that the common ratio of the G.P is 3; Find the first term of the AP and G.P and the common difference of the A.P
(b)The second and third terms of a geometric progression are 24 and 12(x+1) respectively. Given that the sum of the first three terms of the progression is 76, find the whole number value of x and hence the first term
Date posted:
November 8, 2019
.
Answers (1)
-
The diagram below shows a square based pyramid V vertices above the middle of the base. PQ=10cm and VR=13cm M is the midpoint of VR
(Solved)
The diagram below shows a square based pyramid V vertices above the middle of the base. PQ=10cm and VR=13cm M is the midpoint of VR
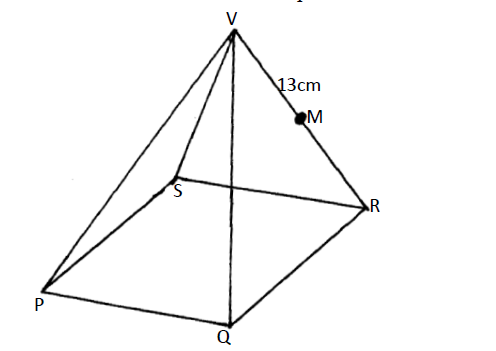
Find
(a)(i) the length PR
(ii) the height of the pyramid
(b)(i) the angle between VR and the base PQRS
(ii) the angle between PM and the base PQRS
(iii) the angle between the planes QVR and PQRS
Date posted:
November 8, 2019
.
Answers (1)
-
Three towns X,Y and Z are such that Y is 50km South of X and Z is on a bearing of 300o from Y. Calculate...
(Solved)
Three towns X,Y and Z are such that Y is 50km South of X and Z is on a bearing of 300o from Y. Calculate the angle XZY given that XZ is 70km.
Date posted:
November 8, 2019
.
Answers (1)
-
A transformation matrix maps an object of area 21cm2 to an image of area 42cm2. Determine the value of p.
(Solved)
A transformation matrix 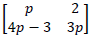 maps an object of area 21cm2 to an image of area 42cm2. Determine the value of p.
maps an object of area 21cm2 to an image of area 42cm2. Determine the value of p.
Date posted:
November 8, 2019
.
Answers (1)
-
A bag contains 2 white balls and 3 black balls. A second bag contained 3 white balls and 2 black balls. The balls are identical...
(Solved)
A bag contains 2 white balls and 3 black balls. A second bag contained 3 white balls and 2 black balls. The balls are identical except for the colours. Two balls are drawn at random, one after the other from the first bag and placed in the second bag. Calculate the probability that the two balls are both white.
Date posted:
November 8, 2019
.
Answers (1)
-
The dimensions of a rectangle are 40cm and 45cm. If there is an error of 5% in the length and 8% in the width. Find...
(Solved)
The dimensions of a rectangle are 40cm and 45cm. If there is an error of 5% in the length and 8% in the width. Find the percentage error I calculating the area of the rectangle.
Date posted:
November 8, 2019
.
Answers (1)
-
Use logarithms correct to 4 decimal places to evaluate.
(Solved)
Use logarithms correct to 4 decimal places to evaluate.
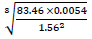
Date posted:
November 8, 2019
.
Answers (1)