-
The diagonal of a rectangular garden measures 11.25m while its width measures 6.75m.Calculate the perimeter of the garden.
(Solved)
The diagonal of a rectangular garden measures 11.25m while its width measures 6.75m.Calculate the perimeter of the garden.
Date posted:
May 2, 2019
.
Answers (1)
-
In the diagram below OX = x and OY = y, M and N are points on OY and XY respectively where OM =1/3 OY...
(Solved)
In the diagram below OX = x and OY = y, M and N are points on OY and XY respectively where OM =1/3 OY and XN =2/5 XY. Lines XM and ON interest at P such that OP =5/9 ON.
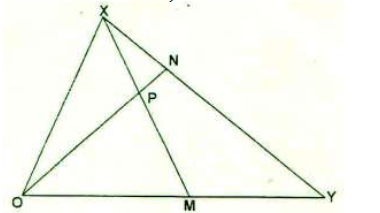
(a) Express in terms of vector x and y.
(i) XY
(ii) ON
(iii) XM
(b) Express XP and PM in terms of x and y
(c) State the ratio XP:PM
Date posted:
April 30, 2019
.
Answers (1)
-
The nth term of a series is given by 6 – 4n.
(Solved)
The nth term of a series is given by 6 – 4n.
(i) Write down the first four terms of the series.
(ii) Find the sum of the first 16 terms of the series.
(iii) Find the 25th term.
Date posted:
April 30, 2019
.
Answers (1)
-
Give that a = 6i, b = 5i – 3j and c = 3i + j, find scalars h and k such that ha +...
(Solved)
Give that a = 6i, b = 5i – 3j and c = 3i + j, find scalars h and k such that ha + kb = c
Date posted:
April 30, 2019
.
Answers (1)
-
Expand and simplify (2 – y)5 and use the first four terms to find the approximate value of (1.8)5 to 2 decimal places.
(Solved)
Expand and simplify (2 – y)5 and use the first four terms to find the approximate value of (1.8)5 to 2 decimal places.
Date posted:
April 30, 2019
.
Answers (1)
-
Points P(2,3) and Q (4,5) are mapped into P1(12,14) and Q1 (22,24) respectively by a transformation matrix T. Find the matrix T.
(Solved)
Points P(2,3) and Q (4,5) are mapped into P1(12,14) and Q1 (22,24) respectively by a transformation matrix T. Find the matrix T.
Date posted:
April 30, 2019
.
Answers (1)
-
Given that Sin theta =5/13,determine the value of tan (90 - theta) without using a calculator or mathematical tables.
(Solved)
Given that Sin theta =5/13,determine the value of tan (90 - theta) without using a calculator or mathematical tables.
Date posted:
April 30, 2019
.
Answers (1)
-
The velocity of a particle after t seconds is given by V = t2 – 4t + 4m/s. Determine the;
(Solved)
The velocity of a particle after t seconds is given by V = t2 – 4t + 4m/s. Determine the;
(a) initial velocity of the particle.
(b) time taken the particle is momentarily at rest.
(c) acceleration of the particle at t = 4.
(d) displacement of the between t = 1 seconds and t = 13 seconds.
Date posted:
April 30, 2019
.
Answers (1)
-
(a) A lamp shade is in the form of a frustum of a cone of diameter 21cm and 28cm. Its height is 10cm.
Calculate the volume...
(Solved)
(a) A lamp shade is in the form of a frustum of a cone of diameter 21cm and 28cm. Find it's height if the height of the cone that was cut off is 10cm.
(b)Calculate the volume of the lampshade.
(c) Two circles each of radius 5cm intersects such that the distance between their centres is 6cm. The
length of the common chord joining the two points of intersection is 8cm. Calculate the area of intersection.
Date posted:
April 30, 2019
.
Answers (1)
-
The cost per kg of Sony Sugar is KSh. 60 and the cost per kg of Imported Sugar is KSh. 80. The two brands of...
(Solved)
The cost per kg of Sony Sugar is KSh. 60 and the cost per kg of Imported Sugar is KSh. 80. The two brands of Sugar are
mixed and sold at a profit of 30% above the cost. If 1kg of the mixture was sold at KSh. 84.50, determine the ratio in
which the two brands were mixed.
Date posted:
April 30, 2019
.
Answers (1)
-
Use the prime factors of 3136 and 2744 to evaluate:
(Solved)
Use the prime factors of 3136 and 2744 to evaluate:

Date posted:
April 30, 2019
.
Answers (1)
-
An aircraft leaves town P ( 30oS, 17oE) and moves directly northwards to Q(60°N, 17°E). It then moved at an average speed of 300 knots...
(Solved)
An aircraft leaves town P ( 30oS, 17oE) and moves directly northwards to Q(60°N, 17°E). It then moved at an average speed of 300 knots for 8 hours westwards to town R. Determine;
a) The distance PQ in nautical miles.
b) The position of town R.
c) The local time at R if local time at Q is 3.12p.m
d) The total distance moved from P to R in kilometers. Take 1 nautical; = 1.853 kilometres.
Date posted:
April 30, 2019
.
Answers (1)
-
A particle P moves in a straight line so that its velocity, V m/s at time t = 0 seconds t is given by V...
(Solved)
A particle P moves in a straight line so that its velocity, V m/s at time t ≥ 0 seconds t is given by V = 28 + t – 2t2. Find.
a) The time when p is momentarily at rest.
b) The speed of P at the instant when the acceleration of the particles is zero.
c) Given that P passes through the point O of the line when t = 0, find the distance of P from O when P is momentarily
at rest.
Date posted:
April 30, 2019
.
Answers (1)
-
Every evening before the end of preps, Eunice either reads a novel or solves a mathematical problem. The probability
that she reads a novel is 4/5.If...
(Solved)
Every evening before the end of preps, Eunice either reads a novel or solves a mathematical problem. The probability
that she reads a novel is 4/5.If she read a novel, there is a probability of 3/4 that she will fall asleep. If he solves a mathematical problem, there is a probability of 1/4 that she will fall asleep. Sometimes the teacher on duty enters Eunice’s classroom. When Eunice is asked whether she had been asleep, there is a probability of only 1/5 that she will
admit that she had been asleep and a probability of 3/5 that she will claim to have been asleep when she had not been asleep
By use of a tree diagram, find the probability that
a) She sleeps and admits
b) She sleeps and does not admit
c). She does not sleep but claims that she had been asleep
d). She does not sleep and says that she has not been asleep
Date posted:
April 30, 2019
.
Answers (1)
-
A man sold a plot of land for sh. 160,000 and invested the money in a bank which pays 12% p.a. compounded semiannually.
After 2 years,...
(Solved)
A man sold a plot of land for sh. 160,000 and invested the money in a bank which pays 12% p.a. compounded semiannually.
After 2 years, he withdrew sh. 100,000 and the left the rest for a further 3 years.
a) How much did she leave in the bank at the end of 2 years?
b) How much did he have in the bank at the end of 5 years?
c) Calculate the total interest made for the whole period.
Date posted:
April 30, 2019
.
Answers (1)
-
The first three terms of a geometric series are 2x,x- 8 and 2x+ 5 respectively.
(Solved)
The first three terms of a geometric series are 2x,x− 8 and 2x+ 5 respectively.
a) Find the possible values of x.
b) For the value of x being an integer, find:
i) The value of the eleventh term
ii) The sum of the first 15 terms
Date posted:
April 30, 2019
.
Answers (1)
-
Two tanks of equal volume are connected in such a way that one tank can be filled by pipe A in 1 hour 20 minutes....
(Solved)
Two tanks of equal volume are connected in such a way that one tank can be filled by pipe A in 1 hour 20 minutes. Pipe
B can drain one tank in 3hours 36 minutes but pipe C alone can drain both tanks in 9 hours. Calculate:
(a) The fraction of one tank that can be filled by pipe A in one hour.
(b) The fraction of one tank that can be drained by both pipes B and C in one hour.
(c) Pipe A closes automatically once both tanks are filled. Assuming that initially both tanks are empty and all pipes
opened at once, calculate how long it takes before pipe A closes.
Date posted:
April 30, 2019
.
Answers (1)
-
A shear parallel to the x-axis maps point (1,2) onto a point (5, 2) .Determine the shear factors and hence state the shear matrix (invariant...
(Solved)
A shear parallel to the x-axis maps point (1,2) onto a point (5, 2) .Determine the shear factors and hence state the shear matrix (invariant line is y = 0)
Date posted:
April 30, 2019
.
Answers (1)
-
An enlargement with centre (-2,3) maps (1,0) onto (4,-3). What is the image of (-3,-6) with the same centre of enlargement
(Solved)
An enlargement with centre (-2,3) maps (1,0) onto (4,-3). What is the image of (-3,-6) with the same centre of enlargement
Date posted:
April 30, 2019
.
Answers (1)
-
A car uses 1 litre of petrol for every 8 kilometres. The car was to travel 480 kilometres and had 15 litre of petrol at...
(Solved)
A car uses 1 litre of petrol for every 8 kilometres. The car was to travel 480 kilometres and had 15 litre of petrol at the beginning of the journey. Each litre of petrol cost sh. 112.00. How much did it cost for the extra petrol added?
Date posted:
April 30, 2019
.
Answers (1)