-
Consider the function
 a) state the singularity of f(z).
b) what is the kind of singularity of f(z).
c) find the Laurent series of f(z).
d) what is the region of convergence of f(z)?.
a) state the singularity of f(z).
b) what is the kind of singularity of f(z).
c) find the Laurent series of f(z).
d) what is the region of convergence of f(z)?.
Date posted:
May 10, 2019
-
a) Integrate z2 along the straight line OM (direct) and also along the path OLM
consisting of two straight line segments OL and LM. O is the origin and M is the
point z = 3 + i.
b) Show that the integral of z2 along the two different paths are equal.
c) Is the result true for any function other than z2 for the two paths?
Date posted:
May 10, 2019
-
Find the fixed points of the bilinear transformation

Date posted:
May 10, 2019
-
Find the fixed points of the bilinear transformation

Date posted:
May 10, 2019
-
a) Find a bilinear transformation, which transforms the unit circle |z| = 1 into the real
axis of the w plane in such a way that the points z1 = 1, z2 = i, z3 = -1 are mapped onto w1 = 0, w2 = 1, w3 = infinite.
b) In what regions the interior and exterior of the circle are mapped.
Date posted:
May 10, 2019
-
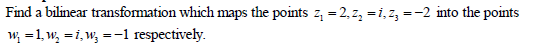
Date posted:
May 10, 2019
-
Find a bilinear transformation which maps the point z = 0, -i, -1 on the z plane into
w = i, 1, 0 respectively on the w plane.
Date posted:
May 10, 2019
-
Explain the nature of the transformation w = z2 considering the semi-circle with centre
the origin and the radius r on the z –plane.
Date posted:
May 10, 2019
-
Let w = 3z + 4 – 5i = f(z)
Find the values of w which corresponds to z = -3 + i on the z plane.
Date posted:
May 10, 2019
-
Find the image of the point (4, 3) on z plane under the transformation w = 2z2 + 3.
Date posted:
May 10, 2019
-
Prove that sin z = sin x cos hy + i cos x sin hy
Date posted:
May 10, 2019
-
Prove that f(z) = 2z2 is continuous at z = z0
Date posted:
May 10, 2019
-
Find the square roots of –15 – 8i
Date posted:
May 2, 2019
-
Solve the equation z4 - 16 = 0
Date posted:
May 2, 2019
-
Express z = 4 + 3i in polar form
Date posted:
May 2, 2019