-
(a) Solve the equation:
(b) A rectangular room is 4m longer than its width. If its area is 12m2, find its dimensions and hence the perimeter of the
room.
Date posted:
April 26, 2019
-
(a) A bus travelling at 99km/hr passes a check-point at 10.00a.m. and a matatu travelling at 132km/h in the same
direction passes through the check point at 10.15a.m. If the bus and the matatu continue at their uniform speeds, find
the time the matatu will overtake the bus.
(b) Two passenger trains A and B which are 240m apart and travelling in opposite directions at 164km/h and 88km/h
respectively approach one another on a straight railway line. Train A is 150 metres long and train B is 100 metres
long. Determine time in seconds that elapses before the two trains completely pass each other.
Date posted:
April 26, 2019
-
A pail is in the shape of a container frustrum with base radius 6cm and top radius 8cm. The slant height of the pail is
30cm as shown below. The pail is full of water.
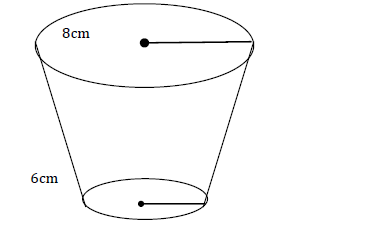(a) Calculate the volume of water.
(b) All the water is poured into a cylindrical container of circular radius 7cm, if the cylinder has the height of 35cm;
calculate the surface area of the cylinder which is not in contact with water.
Date posted:
April 26, 2019
-
Every Sunday Barmao drives a distance of 80km on a bearing of 0740 to pick up her sister Afandi to go to church. The
church is 75km from Afandi’s home on bearing of S500E. After church they drive a distance of 100km on a bearing of
2600 to check on their friend Akoth before Barmao drives to Afandi’s home to drop her off then proceed to her house.
(a) Using a scale of 1cm to represent 10km, show the relative positions of these places.
(b) Use your diagram to determine:
(i) The true bearing of Barmao’s home from Akoth’s house.
(ii) The compass bearing of the Akoth’s home from Afandi’s home.
(c) (i) The distance between Afandi’s home and Akoth’s home.
(ii) The total distance Barmao travel every Sunday.
Date posted:
April 26, 2019
-
The figure below shows two circles of radii 10.5cm and 8.4cm and with centres A and B respectively. The common chord PQ is 9cm.
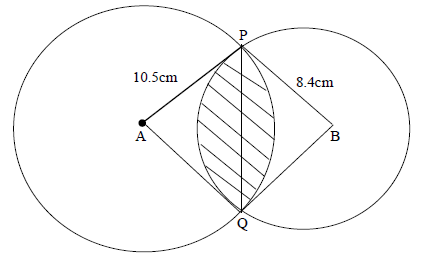(a) Calculate angle PAQ.
(b) Calculate angle PBQ.
(c) Calculate the area of the shaded part.
Date posted:
April 26, 2019
-
Leonorah Jerop was on top of a cliff 30m high sees two boats P and Q out at sea. Both boats were in the same line and
the angle of depression from Leonorah to P was 420 and the angle of depression from Leonorah to Q was 270. Calculate
the distance then between the two boats.
Date posted:
April 26, 2019
-
Express 1.441441........... in the form p/q where p and q are integers. (q # o)
Date posted:
April 26, 2019
-
1.5 litres of water (density 1g/cm3) is added to 5 litres of alcohol (density 0.8g/cm3). Calculate the density of the
mixture.
Date posted:
April 26, 2019
-
Line L1 passes through the points A (1, -2) and B(3, -4). Find the equation of the line L2 passing through the mid-point
of AB and perpendicular to L1, leaving your answer in the form ax + by + c = 0.
Date posted:
April 26, 2019
-
The curved surface area of a cylindrical container is 880cm2. Calculate to one decimal place the capacity of the container in litres given that the height is 17.5cm. (Take π = 22/7).
Date posted:
April 26, 2019
-
Find the angle the line 3y = 2x + 6 makes with the x-axis.
Date posted:
April 26, 2019
-
A man was born in 1956. His father was born in 1928 and the mother three years later. If the man’s daughter was
born in 1992 and the son 5 years earlier, find the difference between the age of the man’s mother and that of his son.
Date posted:
April 26, 2019
-
The marked price of a car in a dealer’s shop was Ksh. 450,000/=. Nasieku bought the car at 7% discount. The dealer
still made a profit of 13%. Calculate the amount of money the dealer had paid for the car.
Date posted:
April 26, 2019
-
The diagram below, not drawn to scale shows part of the curve y = x² + 5 and the line y = 8.2x. The line intersects the
curve at points C and D. Lines AC and BD are parallel to the y-axis.
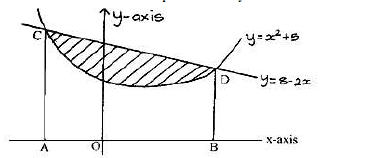(a) Determine the coordinates of C and D.
(b) Use integration to calculate the area bounded by the curve and the x-axis between the points C and D.
(c) Calculate the area enclosed by the lines CD, CA, BD and the x-axis.
(d) Hence determine the area of the shaded region.
Date posted:
April 26, 2019
-
In the figure below O is the centre of the circle. Angle SPQ = 530 and angle PQO = 300.
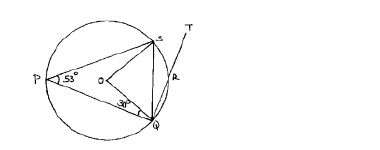(a) Giving reasons find the size of angles:
(i) SOQ.
(ii) PSO.
(iii) SRT.
(b) If the radius of the circle is 14cm, find the area of the quadrilateral OQPS.
Date posted:
April 26, 2019
-
(a) P, Q and R are three quantities such that P varies directly as the square of Q and inversely as the square root of R.
(i) Given that P = 12 when Q = 24 and R = 36, find P when Q = 27 and R = 121.
(ii) If Q increases by 10% and R decreases by 25%, find the percentage increase in P.
(b) If Q is inversely proportional to the square root of P and P = 4 when Q = 3.
Calculate the value of P when Q = 8.
Date posted:
April 25, 2019
-
The G.C.D of three numbers is 30 and their L.C.M is 900. If two of the numbers are 150 and 60, what are the other
three possible third numbers?
Date posted:
April 25, 2019
-
Three angles of a polygon are 1250, 1400 and 1600. The remaining angles are 1450 each. Calculate the sum of the interior angles of the polygon.
Date posted:
April 25, 2019
-
Express in surd form and simplify by rationalizing the denominator.
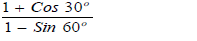
Date posted:
April 25, 2019
-
Expand (1 + 2X)8 in ascending powers of X up to and including the term in X³. Hence evaluate (1.02)8.
Date posted:
April 25, 2019
-
The height and radius of a cone are measured as 21cm and 14.0cm respectively. Taking pi = 3.142, find the percentage error in the volume of the cone.
Date posted:
April 25, 2019
-
(a) Write down the first three terms of the sequence whose nth term is 5n – 2.
(b) The 3rd term of a geometric sequence is 18 and the 6th term is 486. Find the 1st term and the common ratio.
(c) The first and the last term of an AP with 34 terms are 8 and -190 respectively.Find the sum of the first 34 terms.
(d) The 2nd, 4th and 7th term of an AP are the first 3 consecutive terms of a GP. Find the common ratio if the term is 2.
Date posted:
April 25, 2019
-
The diagram below (not drawn to scale) shows the cross-section of a regular hexagonal solid metal prism length
20cm.
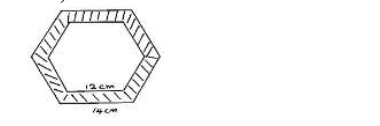Calculate:
(a) the area of the shaded region.
(b) the volume of the material used to make the metal in cm³.
(c) If the density of the metal prism is 3.5g/cm³. Find its mass in kg.
Date posted:
April 25, 2019
-
Construct triangle PQR such that PQ = 7cm, QR = 6cm and RP = 5cm.
(a) Construct the locus of point X which is equidistant from Q and R.
(b) Construct the locus of M which is equidistant from PR and QR.
Mark with letter M the point where this locus meets PQ. Measure QM.
(c) Construct the locus of Y such that PY = 4cm.
(d) Shade the region in which T lies given that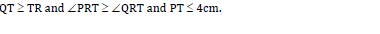 
Date posted:
April 25, 2019
-
a) The numerator of the fraction p/q is increased in the ratio 3:2 while the denominator is decreased in the ratio 2: 3.If the resulting fraction is 27/28, find.
(i) the fraction p/q in its simplest form.
(ii) the percentage change in the fraction.
(b) A piece of work can be done by 30 men in 12 days. They work for 4 days after which 6 of the men leave. How long will
it take the remaining men to complete the job if they work at the same rate?.
(c) Given that the cost of maize is Sh.30 per kg and that of beans is Sh.50 per kg, find the cost of 1kg of a mixture of maize
and beans if they are in the ratio of 3: 2 respectively.
Date posted:
April 25, 2019
-
A matatu left town K at 7.00am and travelled towards town M at an average speed of 60km/hr. A car left town M at 9.00am and travelled towards K at an average speed of 80km/hr. The distance between the two towns is 324km.Find.
(a) the time each vehicle arrived at their destination.
(i) Matatu.
(ii) Car.
(b) (i) The distance the matatu covered before the car started to move from town M to town K.
(ii) The time the two vehicles met on the way.
(c) How far the car was from town K when they met?
Date posted:
April 25, 2019
-
From the roof of a house, a boy can see an avocado tree which is 20m away from the house. He measures the angle of elevation of the top of the tree as 210 and the angle of depression of the bottom of tree as 310. Find the height of the avocado tree.
Date posted:
April 25, 2019
-
A particle moves in a straight line from a fixed point. Its velocity Vmsˉ¹ after t seconds is given by V = 9t² - 4t + 1.
Calculate the distance travelled by the particle during the third second.
Date posted:
April 25, 2019
-
In triangle ABC below, angle ABC = 900, angle ACB = 600, angle ADE = 900, AB = 4cm and BC = BE.
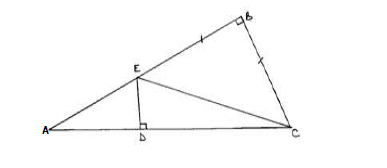Calculate:
(a) BC.
(b) CE.
(c) DC.
Date posted:
April 25, 2019
-
A map has a scale of 1:25000 on this map; a square piece of land is represented by an area of 2cm². Calculate the
actual area, in hectares of the plot.
Date posted:
April 25, 2019