-
Given that Sin x = 3/4 find without using tables or calculators.
a) Cos x
b) Tan (90 - x)
Date posted:
May 3, 2019
-
A polygon of n sides has half of the interior angles 1500 each and the rest 1700 each. Find the value of n.
Date posted:
May 3, 2019
-
If 2/3 is added to the numerator of a certain fraction the fraction will be increased by 1/21 and if 1/2 is deducted
from its denominator that fraction becomes 2/9. Find the reciprocal of the fraction.
Date posted:
May 3, 2019
-
Simplify the expression.
 Hence solve the equation
Hence solve the equation

Date posted:
May 3, 2019
-
Simplify completely

Date posted:
May 3, 2019
-
The position of two towns A and B on earth surface are (360N, 490E) and (360N, 1310W) respectively.Take R = 6370
a) Find the difference in longitude between the town A and B.
b) Calculate the distance between A and B along the latitude in
i) nautical miles
ii) kilometres
c) i) Another town C is 840km East of town B and on the same latitude as town A and B . Find the position of town C.
ii) If the local time in B is 7.30 a.m, find the local time in C.
Date posted:
May 3, 2019
-
The first, third and sixth terms of an arithmetic progression (AP) correspond to the first three consecutive terms of a
geometric progression (GP). The first term of each progression is 16, common difference of AP and d and common
ratio of the GP is r.
a) i) Write two equations involving d and r.
ii) Find the values of d and r.
b) Find the sum of the first 20 terms in the
i) Arithmetic progression (AP).
ii) Geometric progression (GP)
Date posted:
May 3, 2019
-
A company is to construct a parking bay whose area is 135m2. It is to be covered with a concrete slab of uniform
thickness of 150mm. To make the slab, cement, ballast and sand are to be mixed so that their masses are in the ratio 1 :4 : 4. The mass of 1m3 of dry slab is 2500kg. Calculate
a) i) the volume of the slab.
ii) the mass of the dry slab.
iii) the mass of cement to be used.
b) If one bag of cement is 50kg, find the number of bags to be purchased.
c) If a lorry carries 7 tonnes of sand, calculate the number of lorries of sand to be purchased.
Date posted:
May 3, 2019
-
Use method of completing of square leaving your answer in a simplified surds x2 = 7x - 2
Date posted:
May 3, 2019
-
Given matrices A and C as follows;

 Find a matrix B so that BA = c
Find a matrix B so that BA = c
Date posted:
May 3, 2019
-
Find the value of x in the equation 10Cos2x - 7sinx + 2 = 0 for domain 00≤ x ≤ 3600.
Date posted:
May 3, 2019
-
Simplify the following expression as far as possible.
 Hence or otherwise simplified
Hence or otherwise simplified
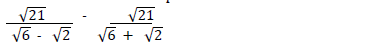
Date posted:
May 3, 2019
-
The vectors a = (2x - 4)i + (x - 3)j + (x - 2)k and the length of /a/ = 7. Find two possible values of x.
Date posted:
May 3, 2019
-
Given that (x - 2) is a factor of 3x2 + kx - 2 find the value of k and hence the other factor.
Date posted:
May 3, 2019
-
a) Expand and simplified the first four terms of the binomial expression (2 - 3x)6.
b) Use the simplified expression in (a) above to estimate the value of (1.97)6 correct 5 decimal places.
Date posted:
May 3, 2019
-
Two values X and Y are such that
3.5 ≤ x ≤ 4.9
0.03 ≤ y ≤ 0.27
What is the greatest possible value of x2/y
Date posted:
May 3, 2019
-
The equation of a circle is x2 - 8x + y2 + 12y = 12. Determine the centre and its radius of the circle.
Date posted:
May 3, 2019
-
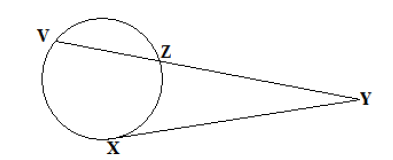
In the figure below XY is a tangent to a circle at YZ.VZ is a chord which produced to meet XY at Y. Given that XY = 9cm
and YZ = 6cm. Calculate the length of VZ.
Date posted:
May 3, 2019
-
Without using mathematical tables evaluate,
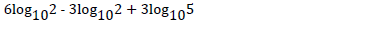
Date posted:
May 3, 2019
-
Make y the subject of the formula.

Date posted:
May 3, 2019
-
Use logarithms to evaluate.
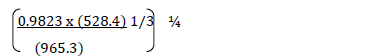
Date posted:
May 3, 2019
-
The distance S metres from a fixed point, covered by a particle t seconds is given by the equation.
s = t3 - 6t2 + 9t + 5.
a) Calculate the gradient of the curve at t = 0.5 seconds.
b) Determine the value of s at the maximum turning point of the curve.
Date posted:
May 3, 2019
-
A bus left town A at 11.45 a.m and travelled towards town B at average speed of 60km/h. A car left town B at 1.15p.m
on the same day and travelled towards town A along the same road at an average speed of 90km/h. The distance
between the two towns is 540km. Determine
a) The time of day when the two vehicles met.
b) How far from A they met.
c) How far outside town B the bus was when the car reached town A.
Date posted:
May 3, 2019
-
The table below shows Kenya’s tax rates in a certain year.
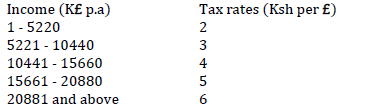 In that year Mr. Mwangi earned a basic salary of Kshs. 16000 per month. He is entitled to a house allowance of ksh.12000 per month and a medical allowance of ksh. 2000 per month.Calculate:
a) i) His taxable income per year in pounds.
ii) His monthly gross tax.
iii) The monthly net tax if he is given a relief of ksh. 1056 per month.
b) Other deductions per month are as follows
N.H.I.F sh. 320, cooperative loan sh. 5600,
WCPS sh 488, coop shares sh 2000
Find his monthly net pay.
In that year Mr. Mwangi earned a basic salary of Kshs. 16000 per month. He is entitled to a house allowance of ksh.12000 per month and a medical allowance of ksh. 2000 per month.Calculate:
a) i) His taxable income per year in pounds.
ii) His monthly gross tax.
iii) The monthly net tax if he is given a relief of ksh. 1056 per month.
b) Other deductions per month are as follows
N.H.I.F sh. 320, cooperative loan sh. 5600,
WCPS sh 488, coop shares sh 2000
Find his monthly net pay.
Date posted:
May 3, 2019
-
The diagram below represents a solid consisting of a hemispherical bottom and a conical frustrum at the top.
 a) Determine the value of x hence the height of the cone.
b) Calculate;
i) The surface area of the solid.
ii) The volume of the solid.
a) Determine the value of x hence the height of the cone.
b) Calculate;
i) The surface area of the solid.
ii) The volume of the solid.
Date posted:
May 3, 2019
-
The figure below shows triangle OAB in which OA = a and OB = b. M and N are points on OB and AB respectively such
that OM = 1/3OB and AN = 2/5AB. Line AM and ON meet at P such that OP = 5/9 ON.
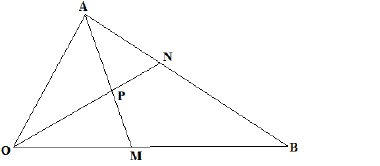 a) Express the following vectors in terms of a and b
i) AB
ii) ON
iii) AM
b) Express AP and PM in terms of a and b,hence show that the points A, P and M are collinear.
a) Express the following vectors in terms of a and b
i) AB
ii) ON
iii) AM
b) Express AP and PM in terms of a and b,hence show that the points A, P and M are collinear.
Date posted:
May 3, 2019
-
Three hundred and sixty litres of a homogenous paint is made by mixing three paints A, B and C. The ratio by volume
of paints A to paint B is 3 : 2 and paint B to paint C is 1 : 2. Paint A costs sh. 180 per litre, paint B sh. 240 per litre and
paint C sh. 127.50 per litre. Determine:
a) The volume of each type of paint in the mixture.
b) The amount of money spent in making one litre of the mixture.
c) The percentage profit made by selling the mixture at sh. 221 per litre.
Date posted:
May 3, 2019
-
The length and breadth of a rectangle are given as (6x - 1) and (x - 2) metres respectively. If the length and breadth
are each increased by 4 metres, the new area is three times that of the original triangle.
a) Form an equation in x and solve it.
b) Find the dimension of the original rectangle.
c) Express the increase in area as a percentage of the original area.
Date posted:
May 3, 2019
-
Evaluate the following

Date posted:
May 2, 2019
-
Work out the following.
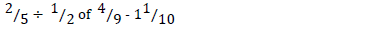
Date posted:
May 2, 2019