-
The diagram below shows a frustum which represents a bucket with an open top diameter of 30cm and a bottom
diameter of 24cm. The bucket is 30cm deep and it is used to fill an empty cylindrical tank of diameter 1.4m and height
of 1.2m.
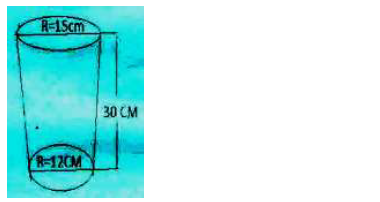(a) Leaving your answer in terms of 𝜋 calculate
(i) The capacity of the bucket in litres
(ii) The capacity of the tank in litres
(b) Determine the number of bucket that must be drawn in order to fill that tank
Date posted:
May 6, 2019
-
The distance between town A and B is 360km. A minibus left A at 8.15 am and travelled towards B at an average
speed of 90km/h. A matatu left B two and a third hours later on the same day and travelled towards A at an average
speed of 110km/hr.
(a) (i) At what time did the two vehicles meet?
(ii) How far from A did the vehicles meet
(b) A motorist started from his home at 10.30 am on the same day and travelled at an average speed of 100km/hr. He
arrived at B at the same time as the minibus. Calculate the distance from A to his house.
Date posted:
May 6, 2019
-
The figure below shows triangle OPQ in which OP = P and OQ = p. M and N are points on OQ and OP respectively such
that ON:NP = 1:3 and OM:MQ = 2:1
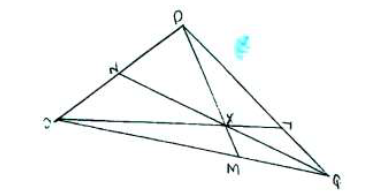(a) Express the following vectors in terms of p and q
(i) PM
(ii) QN
(iii) PQ
(b) Lines PM and QN intersect at X such that PX = hPM and QX = kQN. Express OX in two different ways and hence
find the value of h and k.
(c) OX produced meets PQ at Y such that PY :YQ = 3:2. Using the ratio theorem or otherwise, find OY in terms of P and q
Date posted:
May 6, 2019
-
The number 5.81 contains an integral part and a recurring decimal. Convert the number into an improper fraction and hence into a mixed number
Date posted:
May 6, 2019
-
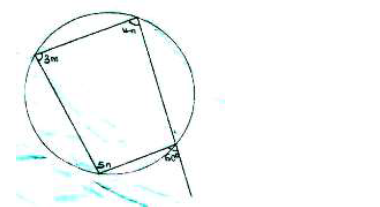
Find the value of m and n in the figure below.
Date posted:
May 6, 2019
-
Solve the simultaneous inequality below.
2x – 5≤ 10 – 3x < x + 18.
Date posted:
May 6, 2019
-
Sales lady sold goods whose marked price was Sh. 340,000 at a discount of 3%. She was paid Sh. 16,490 as a commission for this sale. Calculate the percentage rate of commission she was paid.
Date posted:
May 6, 2019
-
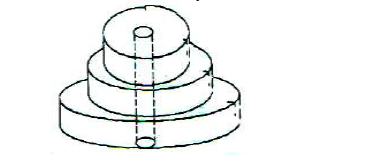
A solid consists of three discs each of 1.5cm thick with diameter of 4cm, 6cm and 8cm respectively. A central hole 2cm
in a diameter is drilled out as shown below. If the density of the material used is 2.8cm3, calculate it mass to 1 decimal place.
Date posted:
May 6, 2019
-
Given that tan x =5/13,find the value of the following without using mathematics tables or a calculator:
(a) Cost x
(b) Sin2(90 – x)
Date posted:
May 6, 2019
-
Given that Log3 = 0.4771 and log 5 = 0.6990, evaluate the following without using logarithm table or calculator.
(a) Log 135
(b) Log 1125
Date posted:
May 6, 2019
-
Mr. Wanyama has a plot that is in a triangular form. The plot measures 170m, 190m and 210m, but the altitudes of the plot as well as the angles are not know. Find the area of the plot in hectares.
Date posted:
May 6, 2019
-
(a) Find the greatest common divisor of the term 9x3y2 and 4xy4.
(b) Hence factorise completely the expression 9x3y2 – 4xy4.
Date posted:
May 6, 2019
-
In a Chemistry experiment, a boy mixed some acid solution of 45% concentration with an acid solution of 25% concentration. In what proportion should the two acids be mixed in order to get 100cm3 of solution of 30% concentration?
Date posted:
May 6, 2019
-
A farmer has a piece of land measuring 840m by 396m. He divides it into square plots of equal size. Find the maximum
area of one plot.
Date posted:
May 6, 2019
-
Simplify the expression.
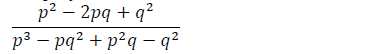
Date posted:
May 6, 2019
-
Evaluate the following;
Date posted:
May 6, 2019
-
Given the equations: y=4 -x2 and y=x2-2x;
a) Find the co-ordinates of the points where the two curves meet. (2 marks)
b) Find the co-ordinates of points where y=4 -x2 meet:
(i) The x-axis.
(ii) The y-axis
c) Find the co-ordinates of the points where y=x2– 2x meet;
(i) The x-axis
(ii) The y-axis
d) Sketch the two curves above on the same axes
e) Find the area enclosed between the curves y=4-x2 and y=x2 – 2x.
Date posted:
May 6, 2019
-
Compete the table below
b) On the same axes draw the graphs of y= sin(x+30)o and y= 2cos(x+30)o.
c) Use your graphs to solve the equation 2cos(x+30)o – sin(x+30)o = 0
d) State the amplitude of each wave.
Date posted:
May 6, 2019
-
The position of two towns P and Q are given to the nearest degrees as P(45oN, 110oW) and Q (45oN, 70oE) Take 𝜋=3.142, Radius of the earth R = 6370km. Find
a) The distance between the two towns along the parallel of latitude in km.
b) The distance between the towns along a parallel of latitude in nautical miles.
c) A plane flew from P to Q taking the shortest distance possible. It took the plane 15 hours to move from P and Q.
Calculate it’s speed in knots
Date posted:
May 6, 2019
-
In the figure below, E is the midpoint of AB, OD:DB=2:3 and F is the point of intersection of OE and AD.
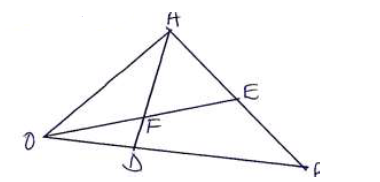a) Given that OA = a and OB = b , express in terms of a and b
i) OE
ii) AD
b) Given further that AF = tAD and OF = sOE where s and t are scalars, find the values of s and t.
c) Show that O, F and E are collinear.
Date posted:
May 6, 2019
-
a) PQRS is a quadrilateral with vertices p(1, 4) Q(2, 1), R(2, 3) and S(6, 4). On the grid provided plot the quadrilateral
b) Draw P1Q1R1S1 the image of PQRS under a positive quarter turn about the origin and write down its co-ordinates.
c) Draw P11Q11R11S11 the image of P1Q1R1S1 under the transformation whose matrix is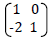 
and write down its co-ordinates.
d) Determine the matrix T of a single transformation that maps PQRS onto P11Q11R11S11
Date posted:
May 6, 2019
-
In a geometrical progression, the sum of the second and third terms is 6; and the sum of the third and fourth terms is -12. Find:
a) (i) The first term
(ii) The common ration
b) The sum of number of consecutive terms of an arithmetical progression is -19 ½ ; the first term is 16 ½ ; and the common difference is -3. Find the number of terms.
Date posted:
May 6, 2019
-
The table below shows the number of students who scored marks in mathematics test.
a) Draw a cumulative frequency graph for the data.
b) Use the graph to estimate the median mark.
c) If students who score over 40 marks pass the tests estimate the percentage of the students
i) who passed
ii) who failed
Date posted:
May 6, 2019
-
X and Y are two variables such that Y is partly constant and partly varies inversely as the square of X. If Y = 3 when X= 2 and Y = 5 when X = 1, find Y when X = 4.
Date posted:
May 6, 2019
-
Make y the subject of the formula given
Date posted:
May 6, 2019
-
The equation of a circle centre (h, k) is 2x2 + 2y2– 8x + 5y + 10 = 0. Find the values of h and k.
Date posted:
May 6, 2019
-
Find the midpoint of the straight line joining A (2, 1) and D (6,5).
Date posted:
May 6, 2019
-
Without using mathematical tables or calculator; evaluate:
Date posted:
May 6, 2019
-
Find the equation of the normal to the tangent of the curve y=x3 – 3x2 + 2x + 1 at the point where x=3. Leave your answer in the form y=mx + c.
Date posted:
May 6, 2019
-
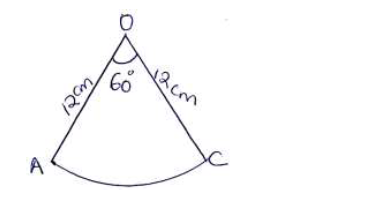
The sector below has a radius of 12cm and an angle AOC = 60o is folded to form a cone. Find the volume of the cone
formed.
Date posted:
May 6, 2019