-
Given that 84y x 27x = 36, find the exact values of x and y.
Date posted:
May 6, 2019
-
The area of a rhombus is 120 cm2. Given that one of its diagonals is 24cm, calculate the perimeter of the rhombus.
Date posted:
May 6, 2019
-
Simplify the expression:
Date posted:
May 6, 2019
-
Use tables of squares, square root and reciprocals to evaluate to 3 decimal places the question below.
Date posted:
May 6, 2019
-
Evaluate without using a calculator
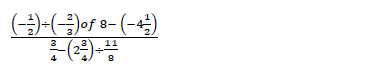
Date posted:
May 6, 2019
-
The figure shows triangle OPQ in which QN : NP = 1 : 2, OT : TN = 3 : 2 and M is the mid - point of OQ.
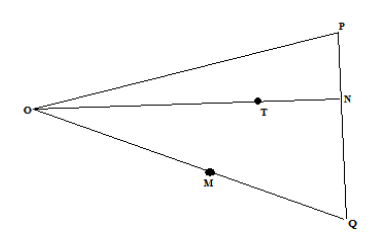OP = p and OQ = q
a) Express the following in terms of p and q.
i) PQ
ii) ON
iii) PT
iv) PM
b) Hence show that P, T and M are collinear.
Date posted:
May 6, 2019
-
The table below shows income tax rates for a certain year.
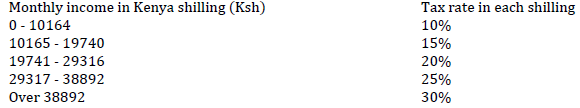A secondary school teacher was earning a monthly basic salary of Ksh. 55,480 house allowance of Kshs. 12,000 and a
commuter allowance of ksh. 8000. He was entitled to a personal relief of Kshs. 1162 per month.
a) Calculate
i) The teacher’s taxable income.
ii) The teacher’s net monthly tax.
b) In addition to the tax the other deductions were per month as follows:
- Cooperative loan Ksh. 10,000
- Co-operative shares Ksh. 2,000
- Window and children’s pensions scheme at 2% of the basic salary.
Calculate the teacher’s net monthly pay.
Date posted:
May 6, 2019
-
The figure below shows the pulleys with centres A and B and radii 13cm and 6cm respectively. The distance between
the centres is 25cm.
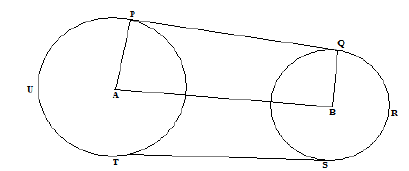A belt PRSTUP goes round the two pulleys. PQ and TS are also tangents.
a) Calculate
i) Length PQ
ii) Angle BAP
b) Hence or otherwise calculate the length of the belt.
Date posted:
May 6, 2019
-
A businesswoman mixes three types of rice A, B and C in the ratio A : B = 1 : 2 and B : C = 4 : 5. The mixture is to
contain 60 bags of type B.
a) Find the ratio A : B : C
b) Find the required number of bags of type C.
c) The cost per bag of type A is Kshs. 7,500, type B Kshs. 5,000 and type C Kshs. 4,000.
i) Calculate the cost per bag of the mixture.
ii) Find the percentage profit if the selling price of the mixture is Ksh. 6,500 per bag.
Date posted:
May 6, 2019
-
The gradient function of a curve is x3 - 4. If the curve passes through point (2, 3). Find the equation of the curve.
Date posted:
May 6, 2019
-
A plane flies from point P (400N, 500E) towards West to a point Q. Given that the plane covers a distance of 10,000km what is the position of Q. (Take 𝜋= 22/7, radius of the earth 6370km)
Date posted:
May 6, 2019
-
Francis bought a vehicle at ksh. 2 800 000. After three years he sold the vehicle at Kshs. 1,500,000. Determine the average rate of depreciation per annum correct to one decimal place.
Date posted:
May 6, 2019
-
Solve the simultaneous equations.
2x - y = 3
xy - y2 = 0
Date posted:
May 6, 2019
-
The figure below represent a square based right pyramid ABCDV. AB = 10cm,AV = BV = CV = DV = 15cm.
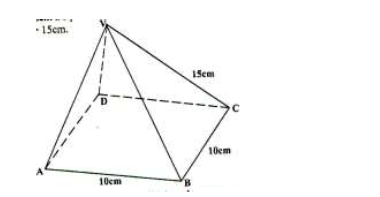Calculate the angle between AV and the base ABCD to the decimal place.
Date posted:
May 6, 2019
-
Solve for x without using mathematical tables or calculators.
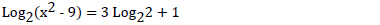
Date posted:
May 6, 2019
-
Expand (4 - x)7 upto to the term in x4. Hence find the appropriate value of (3.8)7.
Date posted:
May 6, 2019
-
In a transformation, an object with area 9cm2 is mapped onto an image whose area is 54cm2. Given that the matrix of transformation is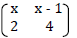 
find the value of x.
Date posted:
May 6, 2019
-
Determine the amplitude and period of the function 3y = 6sin (2x - 30).
Date posted:
May 6, 2019
-
The table shows the frequency distribution of marks scored by students in a test.
Determine the median mark correct to one decimal point.
Date posted:
May 6, 2019
-
The quantities P, Q and R are such that P varies directly as Q and inversely as the square of R. Given that P = 2 when Q = 12 and R = 6. Determine the equation connecting the three.
Date posted:
May 6, 2019
-
In the figure below PQR is the diameter of the circle centre O. Angle QPR = 200 and angle QTR = 800
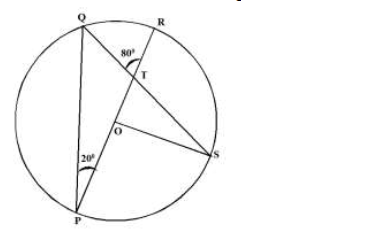Determine the size of
a) Reflex angle POS
b) Angle OSQ
Date posted:
May 6, 2019
-
The first term of an arithmetic sequence is 5 and the common difference is 2.
a) List the first six terms of the sequence.
b) Determine the sum of the first 40 terms of the sequence.
Date posted:
May 6, 2019
-
The figure below shows a right pyramid VEFGHK. The base EFGHK is a regular pentagon. EO = 7cm and VE = 12cm.
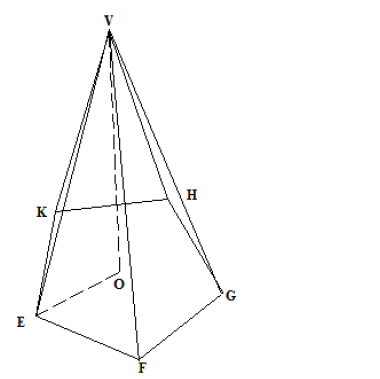Calculate
a) The perimeter of the base to 2 decimal places.
b) The length VO to 2 decimal places.
c) The angle which edge VF makes with the edge FE.
d) The volume of the pyramid to 2 decimal places
Date posted:
May 6, 2019
-
The figure below represents a game sanctuary in the shape of a quadrilateral in which AB = 30km,AE = 20km and CE = 45km 0, 0 and 0.
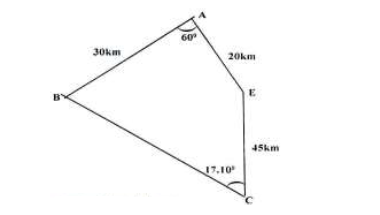Calculate
a) The side BC correct to 2 decimal places.
b) The angle ABE to 1 decimal place.
c) The area of the game sanctuary in hectares correct to 2 decimal places.
Date posted:
May 6, 2019
-
A calf runs in a straight line towards a cow with a velocity of vm/s after t seconds given by v = t (8 - t).
a) Complete the table below
b) Calculate the distance covered by the calf.
i) Using eight trapezia of equal width.
ii) Using the exact method.
Date posted:
May 6, 2019
-
The percentage marks obtained by 40 students in a test are as under:
85, 30, 49, 62, 17, 84, 24, 15, 82, 61, 74, 38, 27,...
Solved
The percentage marks obtained by 40 students in a test are as under:
85, 30, 49, 62, 17, 84, 24, 15, 82, 61, 74, 38, 27, 13, 44, 72, 61, 49, 38, 23,
90, 32, 67, 18, 45, 58, 22, 46, 37, 39, 43, 55, 62, 30, 46, 59, 41, 26, 34 and 47.
a) Prepare a grouped frequency table from the above data using a class width of 10.
b) Use 49.5 as the working mean and estimate the mean from the grouped frequency table.
c) Prepare a cumulative frequency table and draw the cumulative frequency curve on the grid of squares provided.
Date posted:
May 6, 2019
-
Use this velocity - time graph which represents the motion of a car for 10 seconds, to find:
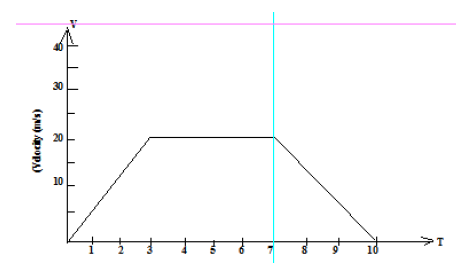a) The rate of acceleration.
b) The rate of retardation.
c) The total distance travelled.
d) The total distance travelled during the first 4 seconds.
e) The average speed maintained during this journey.
f) The distance travelled at the constant speed.
Date posted:
May 6, 2019
-
A line T passes through points (-3, -5) and (3, -6) and is perpendicular to a line l at (-2, -2).
a) Find the equation of l.
b) Find the equation of T in the form ax + by = c where a, b and c are constants.
c) Given that another line Q is parallel to T and passes through (1, -3) find x and y intercepts of Q.
d) Find the points of intersection of L and Q.
Date posted:
May 6, 2019
-
Maina can do a piece of work in 12 hours. Muthui can do it in 20 hours. How long would it take Muthui to complete the work if Maina has been working for 7 hours.
Date posted:
May 6, 2019
-
A point A (-1, 3) is mapped onto A1(8, 12). Fidn the centre of enlargement given that the scale factor is 2.
Date posted:
May 6, 2019