-
Two machines M and N produce 60% and 40% respectively of the total number of items manufactured in a factory. It is observed that 5% of items produced by machine M are defective while 3% of the items produced by machine N are defective. If an item is selected at random from the factory, find the probability that it is defective.
Date posted:
November 20, 2019
-
Trains A and B are moving in opposite directions on parallel tracks. Train A is 56 metres long and is moving at a speed of 63km/h. Train B is 90 metres long and is moving at a speed of 45km/h. The two trains are about to start passing each other. Calculate the time, to the nearest second, that they will take to completely pass each other.
Date posted:
November 20, 2019
-
ABCD and MNPQ in the figure below are two shutters of a window. The shutters are identical and square in shape. Both shutters are opened through an angle of 58°.
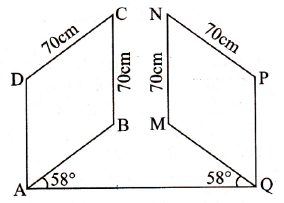If each edge of the shutter is 70cm long, find the shortest distance from C to M.
Date posted:
November 20, 2019
-
Using matrices solve the following pair of simultaneous equations
6y − 2x + 20 = 0
3x − 7y − 26 = 0
Date posted:
November 20, 2019
-
Two taps, A and B, when opened at the same time can fill a tank in 3 hours 36 minutes. Tap A working alone takes 3 hours longer than Tap B to fill the tank. How many hours does it take Tap A alone to fill the tank?
Date posted:
November 20, 2019
-
Point M is the midpoint of a straight line XY. If the position vectors of Y and M are 3i + 4j − 2k and 3j − 0.5k respectively. Find the position vector of X, hence the magnitude of XY.
Date posted:
November 20, 2019
-
Without using mathematical tables or calculators, simplify
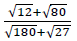
Date posted:
November 20, 2019
-
Each side of a regular heptagon measures 11.2cm. What is the percentage error in calculating the heptagon’s perimeter?
Date posted:
November 19, 2019
-
Using completing the square method, solve
10x2 − 11x − 6 = 0
Date posted:
November 19, 2019
-
The figure shows a water tank which consists of a hemispherical part surmounted on top of a cylindrical part. The two parts have the same diameter of 2.1 M and the cylindrical part is 1.5 m high as shown. All surfaces of the tank are made of iron sheets. (Take π = 22/7)
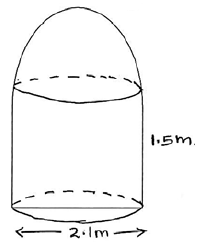(a) Allowing for 15% wastage in overlapping, calculate to 2d.p the area of iron sheets required.
(b) Ironsheet costs sh.400 per square meter while labour and other. Materials amountsto 50% of the cost of ironsheets. Find the cost of constructing the tank.
(c) Calculate the (i) volume of the tank in m3
(ii) capacity of the tank in litres.
Date posted:
November 19, 2019
-
Lines L1 is given by equation y = -2x +4 and L2 is 3x- y=1 intersect at T.
(a) Determine the co-ordinates of T.
(b) Another line, L3 is perpendicular to line L2 and passes through point N(5,8).Determine its equation and leave the answer in the form of ax + by=c where a, b, and c are integers.
(c) Determine the equation of a perpendicular bisector of a line segment passing through points T and N.
Date posted:
November 19, 2019
-
Three towns PQR are such that Q is 20km in the bearing of 045° from P while R is 27.5 km in the bearing of S20°E from Q.Using the scale of 1cm rep 5km.
(a) Determine the actual distance between P and R.
(b) State the true bearing of P from R.
(c) Show a point x which is equidistant from the three towns.
(d) Determine the actual distance from x to town R.
Date posted:
November 19, 2019
-
On a certain map, an estate is represented by an area of 48cm2. If the actual area of the estate is 1200Ha, find the scale of the map in the form 1: n.
Date posted:
November 19, 2019
-
Using tables of reciprocals evaluate
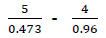
Date posted:
November 19, 2019
-
Given that tan (90-x) = 3/4 without using calculators or tables,
Find: (i) Sin x
(ii) Cos (90 – x)
Date posted:
November 19, 2019
-
The diagram below shows a region R bounded by 3 lines L1, L2 and L3
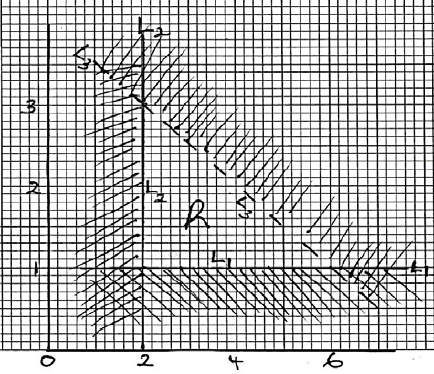Determine the 3 inequalities satisfied by the region marked R.
Date posted:
November 19, 2019
-
James left sh 430,500 to be shared by his wife, daughter and son in the ratio of 2:1:3 respectively. His wife decided to divide her share equally between her daughter and son. Find how much the daughter finally got.
Date posted:
November 19, 2019
-
Last year, Onyango was four times as old as his son, in four years time, the sum of their ages will be 53. Determine their present ages.
Date posted:
November 19, 2019
-
Three numbers are such that m2n3k = 360. Find m, n, and k.
Date posted:
November 19, 2019
-
Agotho has a rectangular plot that was measured to the nearest meter and found to be 80m in length and 60m in width. Determine the percentage error in its perimeter.
Date posted:
November 19, 2019
-
Evaluate without using Mathematical tables or a calculator.
2log5 - 1/2 log16 + 2 log40
Date posted:
November 19, 2019
-
The region R in the figure below is defined by the inequalities L1, L2 and L3.
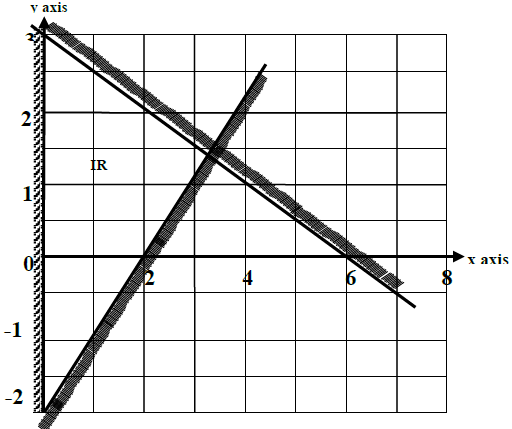Find the three inequalities.
Date posted:
November 19, 2019
-
A regular polygon has internal angle of 1500 and side of length 10cm.
(a) Find the number of sides of the polygon.
(b) Find the perimeter of the polygon.
Date posted:
November 19, 2019
-
In a carton there are 8 red pens, 5 blue pens and 2 green pens. Two pens are picked at random
from the carton without replacement.
a) Draw a probability three diagram to represent this information.
b) Use the tree diagram to find the probability that:
i) The first pen picked is red.
ii) The first pen picked is blue or green.
iii) The two pens picked are blue.
iv) At least one of the pens picked is green.
Date posted:
November 19, 2019
-
An airplane leaves town A(400N,1550W) and flys to town B(400N,250E) using the shortest route and at a speed of 450 knot (Take 𝜋 =3.142 and radius of the earth R=6370km.)
(a)i) Calculate the distance between A and B covered by the airplane in nautical miles.
ii) Calculate the time taken by the aeroplane to fly from A to B.
(b) From B the plane flies westwards along the latitude to a town C(400N, 130W). Calculate the distance BC in kilometres.
(c) From town C, The plane took off at 3:10 p.m towards town D(100N, 130W) at the same speed. At what time did the plane land at D?
Date posted:
November 19, 2019
-
A car hire company hire out cars such that there is a fixed charge and another part which varies with the distance covered. Taking C to stand for total cost, d for distance covered, k for fixed charge and t for charge per kilometer.
a) Express C in terms of k,tand d.
b) Given that the total cost is 7000 when the distance is 200km and the total cost is 11000 when distance is 400km.
i) Find the values of k and t.
ii) Find the equation connecting c,t,k and d.
(c) Find the cost of hiring a car to area a distance of 500km.
(d) Due to increase in fuel prices, the company increased the fixed charge by 20% and charge per kilometer by 10%:
i) Find the cost of hiring the car for 500km.
ii) Find the percentage increase of hiring the car for the 500km.
Date posted:
November 19, 2019
-
Find the centre and the radius of a circle whose equation is x2 + y2 + 6y − 8x − 2y = 0.
Date posted:
November 18, 2019
-
Find the value of x that satisfies the equation. log(z+5)=log4 –log(x+2).
Date posted:
November 18, 2019
-
The length of a rectangle is (x+1) cm. its width is 3cm shorter than its length. Given that the area of the rectangle is 22cm, find its length using completing the square method.
Date posted:
November 18, 2019
-
Make A the subject of the formula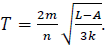 
Date posted:
November 18, 2019